| View this file in " .pdf " format |
When we talk about making a room “sound right”,
we are probably dealing with room acoustics as a science
acoustics has been around for about hundred years. Until
then good acoustics happened by experiment, by experience,
or simply by accident..
Today we know a lot about the parameters that influence
the “sound” of a room.
Talking about the control room we know that basically this
room should act as neutral as possible. But this is not
always the case. Lets just take a short look on some of
the issues, than one must be aware of. |
|
Good acoustics
Here is a list of important parameters concerning good
acoustics.
» Proper reverberation time
» Good sound distribution
» Adequate sound pressure level
» Low background noise level
» No echo (flutter echo)
Now lets have a look on these headlines that will be adequate
for the most purposes concerning sound production. |
|
|
TÓPICS
» Reverberation Time
» Sabine formula
» Room
modes
» How does the
standing waves unfluence the sound fields?
» Standing
Waves
» Absorbent Materials
» Diffusors
» Comb Filtering
» Rear wall cancellation |
|
|
|
The reverberation time is defined by the time it takes a
sound to attenuate 60 dB after the source is stopped. In
the real life we can experience reverb times from approximately
0 sec. (outdoors or in anechoic chambers) to something like
10 – 12 sec. In special reverb chambers the time may
exceed 20 sec. Control rooms normally should have a reverb
time around 0.2 – 0.3 sec.
Why do we have reverberation? The speed of the propagating sound wave is very slow –
at least compared to light: approx. 1130 ft. or 340 m per
sec.
|
|
If there are no reflecting surfaces between the sound source
and our ears, only the direct sound is heard and there is
no reverberation.
If there is a single reflecting surface we may hear the
reflected sound in one way or another, but there is still
no reverberation.
If the sound is generated in a room, there are a whole lot
of reflections. Each of these travels different paths with
different distances on the wayto the receiver. Each time
the sound hits a surface it may loose some energy if the
surface is absorbing.
|
|
| |
|
|
|
|
|
| |
|
|
|
|
One sound source, one receiver and
no room. Only the direct sound is received |
|
One sound source, one receiver,
and one reflecting surface. The sound is received twice.
(In the control room this is normally experienced as comb
filtering, see later). |
|
One sound source and one receiver
in a room. The sound impulse is reflected in many surfaces
All the reflections are melting together and heard as
reverberation. |
|
|
|
Sabine is the father of modem acoustics. He found that reverberation
time is described by a relationship between the room size
and the amount of absorption in the room. Larger rooms –
longer reverberation. More absorption – shorter reverberation.
T = 0,161 x V / A
Where
T: Reverberation time in
seconds
V: Volume in m3
A: Absorption in m2 Sabine
0,161: Is a constant (to
make the calculation right with the actual units)
|
|
Note:One square meter (1 m2) Sabine is comparable to an
open window with an area of one square meter:
The sound that hits the window will disappear and never
return. One square meter Sabine is one square meter with
full absorption. The basic formula sounds simple, but the
problem is that the materials in the room will absorb differently
at different frequencies. The absorption may range from
nothing (fully reflective) to total absorption.
A proper reverb time should be constant with frequency,
but this is not always the case because of the behaviour
of the materials in the room. The low frequencies are the
most difficult to control.
This is why the reverberation time against frequency in
practice may look like this:
|
|
| |
|
|
Reverberation time measured in a control
room. From 250 Hz and above the curve is nicely placed around
3 sec. But belov the reverb time rises to 75 sec. which
is too much. |
|
|
|
|
| All materials in the room act acoustically
even if they are not so-called acoustical materials. Basically we
have three kinds of absorbers. |
Membrane absorbers
This kind of absorber includes wooden floors, windows, doors,
etc. This absorber provides absorption in the low end of
the frequency range. The efficiency is normally not very
high, but under normal conditions large areas are included
in the basic room construction. Special designed membrane
absorbers can be very effective.
Resonance Absorbers
Resonance absorbers include slit panels, perforated plate,
Helmholtz resonators etc. These absorbers are normally used
in the frequency midrange. The absorption is medium to high.
Holes or cracks
Mineral wool or similar
|
|
Porous absorbers
These absorbers include mineral wool, carpets, curtains,
and so on. They can be very effective, but the thickness
of the material has to be taken into account. Thin layers
will only absorb the highest frequencies. (Think of a rehearsal
room in the concrete basement where the only damping is
a carpet on the door: Not good at low frequencies!).
To absorb a given frequency (and all frequencies above)
the thickness of the absorber must be the quarter of the
wavelength of that frequency. Or: the front of the material
must be placed at a distance of one quarter of the wavelength.
|
|
|
|
 |
|
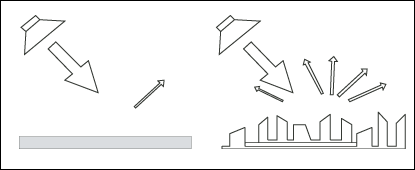
A diffuser provides diffuse
reflection of the sound radiated against it. It can be a
very useful solution in cases where reflections are disturbing
the sound image and it is not advisory to ad further absorption.
So in order to reduce flutter echoes, comb filtering etc.,
special elements can be placed on the “disturbing”
surface. These elements must have dimensions comparable
to the frequencies at which diffusion is wanted.
Absorption or diffusion? |
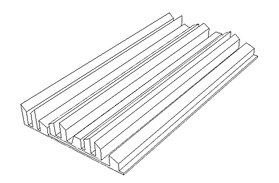
A special technique developed by Manfred Schroeder is very
capable in making a smooth and controlled diffusion. These
diffusers normally referred as the "Woodiffusor"
can be found as prefab modules.
Cross section of one example of the ."Woodifusor"
Jocavi
|
|
 |
|
|
|
Standing waves exist in all kind of rooms. The shape of
the room, the dimensions of the room, and the relationship
between the dimensions of the room, are important parameters
that will determine the frequencies around which the phenomenon
exists as well as the distribution of these standing waves.
But how do they occur?
Imagine a sound source. When the sound is emitted the
sound is emitted the sound wave will propagate in all
directions if no obstacles in sight. This will of course
happen with the speed of sound. Now, if the sound source
is placed inside a room the sound wave will hit the boundaries
of the room.
If the boundaries consist of acoustically hard (reflective)
surfaces, the sound is reflected. If the angle of incidence
is 90º the sound will be reflected right back where
it came from. Under certain circumstances the sound wave
will meet itself again. For instance if the sound is reflected
between to parallel walls.
|
|
This Becomes a problem, when the sound wave not only meets
itself, but when it meets itself in phase. And this will
happen when the distance between the walls is half a wavelength
of the radiated sound wave. Or one whole wavelength –
or 1 ½, 2 ½ and so on.
This phenomenon is called standing waves. Actually the
sound wave is not standing. But it is experienced like
that because the sound pressure maxima and minima are
positioned in fixed places in the room.
The sound field is initially radiated having a radical
wave front but within a few reflections the sound field
has obtained a plane wane front.
|
|
|
|
| The special frequencies are also called room modes.
Standing waves between parallel walls are called axial modes. Other
modes exit. For instance tangential and radical modes. (See the
illustration). Normally the axial modes are the strongest. |
|
| |
The standing waves are characterized by having a maximum
sound pressure at the boundaries of the room. Depending
on the frequency there are one or more dips across the
room. In a box shaped room the frequencies can be calculated
as follows:
where :
f = frequency in Hz
c =speed of sound (approx. 340 m/s or 1130 ft/s)
l = length of the room
w = width of the room
h = height of the room
n = integer from 0 and up
|
|
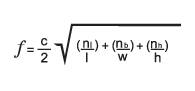
|
|
| |
|
|
| HOW DOES THE STANDING WAVES UNFLUENCE
THE SOUND FIELDS? |
|
|
The maxima
of the standing waves are shown in the figure. The curve
expresses the area of the room where the actual frequency
is audible. At the minima the frequency is represented at
a much lower level (sometimes – 40 dB compared to
the maximum).
If the room has the same dimensions as length, width,
and even height it is very problematic to obtain an even
sound distribution.
|
|
How to prohibit standing waves?
Parallel walls in the room should be prevented. Then the
strongest modes are suppressed. When placing the monitors
it is important that as few modes as possible are excited.
This is why the monitors should not be placed in a maximum
of a standing wave. At low frequencies a monitor can be
considered as to radiate the sound energy in all directions. |
| |
|
|
|
|
|
This is also called a 4  radiation
When placing the monitor close to a solid boundary –
for instance a wall – the sound energy that should
have been radiated in the direction of the wall instead
is radiated into the free half space. Hence the sound pressure
is doubled in the half space, which yields +6 dB. |
|
This is also called a 2  radiation
When placing the monitor close to a solid boundary –
for instance a wall – the sound energy that should
have been radiated in the direction of the wall instead
is radiated into the free half space. Hence the sound pressure
is doubled in the half space, which yields +6 dB. |
| |
|
|
|
|
|
This is also
called  radiation.
Placing the monitor against two boundaries – for instance
in a corner limited by two walls – it is now radiating
to the quarter space. Now the sound pressure is doubled
twice, which yields +12 dB. |
|
This is also called  /2
radiation..
In practice, the placing by barrier walls, or ground, influence the frequency range below 125-150 Hz. |
|
|
|
| |
|
|
|
|
The filtering function that arises
when a signal is added to itself after having been delayed
in time is called a comb filter. The resulting frequency
response resembles a comb, hence the name. |
| |
|
|
|
|
Two 500 Hz sinusoidal tones added.
The second tone is delayed 1 ms hence the sum is zero. Two
1 kHz sinusoidal tones added. The second tone is delayed
1 ms hence the sum is the double (+6 dB). |
|
The comb filter function is
almost never intentional, but it is heard all the time in sound
productions, where it can arise both acoustically and electrically.
Acoustically, it typically occurs when the sound on its way from
source to recipient takes in part a direct path and in part an
indirect path via a single reflective surface. The reflection
must be attenuated at least 10 dB and preferably 15 dB in order
for it not to have an effect on the sound field at the recipient
position. Electrically, the phenomenon arises when two microphones
with a certain distance between them capture the same signal and
the level from each microphone is of the same order of magnitude. |
|
|
Two typical situations
in which comb filters arise, either acoustically or electrically.
In general: All digital signal processing takes time.
This means in practice that comb filter effects can arise
if you loop a signal via, for example, a compressor and
combine this signal with the original. |
| |
|
|
dB
Level Frequency– Hz
An example of a comb filter created by the combining
of two signals with the same amplitude, but with a time
delay between them of just 1 ms.
It can be seen that a dip occurs due to cancellation at
500 Hz, 1.5 kHz, 2.5 kHz, etc. It can also be seen that
the two signals add to double their value (+6 dB) at low
frequencies and with a full wavelength’s delay at
1 kHz, 2 kHz, 3 kHz etc.
Dip Frequency
Cancellation occurs for a comb filter at all the frequencies
where the two signals are in opposite phase. This occurs
when the time delay comprises duration of ½, 1
½, 2 ½, etc. periods. At 1 kHz the period
is 1 ms. Half of the period is 0.5 ms. If a time delay
of precisely 0.5 ms occurs, it means that cancellation
will arise, not just at 1 kHz, but also at 2 kHz, 3 kHz,
4 kHz etc |
|
|
|
|
|
| |
|
|
When the monitor is set up at some distance in front
of a wall, reflections from the wall may occur and influence
the perceived frequency response. This could result in
comb filtering if all frequencies produced by the monitor
were radiated in all directions. But the monitors are
typically only omni- directional at low frequencies. The
result of the reflection is a single or few dips in the
frequency response perceived in front of the monitor.
The frequency response may look like this: one cancellation
at the frequency that has a wave length of four times
the distance to the rear wall.
The dip – or cancellation frequency – is dependent
on the distance to the wall. If the distance is 1 m, the
first dip frequency with a wavelength of 4 m.
l = c/f
Where :
l = wavelength (m) (ou
ft)
c = speed of sound [m/sec]
(or ft./sec.)
f = frequency (Hz) |
 |
 |
Hence:
4 = 344 / f
F = 86 Hz |
A closer position will result in a cancellation at a
higher frequency. This is then limited by the frequency
where the monitor becomes directional and does rot radiate
sound to the rear.
A farther position will result in cancellation at a lower
frequency. This is limited by the distance being so long,
that the reflected sound is attenuated due to the long
extra path travel.
|
|
| View this file in " .pdf " format |